مساله:
یک مرد (اجازه دهید او را Eulampy بنامیم) مجموعه ای از تخم مرغ های Fabergè تقریبا مشابه دارد. یک روز دوست وسوسه گرش به او گفت:
- آیا آن آسمان خراش را می بینی؟ و آیا می توانی حداکثر طبقه را به من بگی که اگر تخم مرغ خود را از آن بیندازی، آن نمی شکند؟
- Eulampy گفت: نه
- وسوسه گر گفت: اما اگر شما N تخم مرغ به من بدهید، من به شما جواب رو می گم.
- Eulampy گفت: قبوله. اما من قبل از شروع این کار یک شرط دارم: اگر من بیش از m خطا در تخم مرغ ها ببینم، قلب من به جای تخم مرغ میشکند. بنابراین شما فقط M تلاش برای انداختن تخم مرغ دارید. آیا می توانید یک طبقه دقیق با این محدودیت به من بگویید؟
وظیفه:
شما باید وسوسه گر را کمک کنید (تابعی بنویسید):
height :: Integer -> Integer -> Integer height n m = -- see text
این تابع دو ورودی دارد – n تعداد تخم مرغ ها و m تعداد تلاش های مجاز- باید حداکثر ارتفاع آسمان خراش را حدس بزنید (در طبقات) که در آن تضمین دهید بالاترین طبقه ای هست که اگر تخم مرغ را از آنجا انداختید نمی شکند.
به این صورت که:
- هربار می توانید یک تخم مرغ را از طبقه خاصی پرتاب کنید
- تمام تخم مرغ ها شبیه هم هستند و پایداری یکسانی دارند (که اگر از یک طبقه خاص و پایین تر از آن انداخته شوند نمی شکنند و در غیر اینصورت می شکنند)
- شما n تخم مرغ دارید و m شانس برای انداختن
- حداکثر ارتفاع چقدر است به طوری که همیشه می توانید تعیین کنید که طبقه مورد نظر کدام طبقه است در صورتی که طبقه هدف می تواند هر طبقه بین 1 تا این حداکثر ارتفاع باشد؟
مثال ها:
height 0 14 = 0 height 2 0 = 0 height 2 14 = 105 height 7 20 = 137979
محدوده داده ها:
n <= 20000 m <= 20000
Description:
One man (lets call him Eulampy) has a collection of some almost identical Fabergè eggs. One day his friend Tempter said to him:
Do you see that skyscraper? And can you tell me a maximal floor that if you drop your egg from will not crack it?
No, – said Eulampy.
But if you give me N eggs, – says Tempter – I’l tell you an answer.
Deal – said Eulampy. But I have one requirement before we start this: if I will see more than M falls of egg, my heart will be crushed instead of egg. So you have only M trys to throw eggs. Would you tell me an exact floor with this limitation?
Task
Your task is to help Tempter – write a function
height :: Integer -> Integer -> Integer height n m = -- see text
that takes 2 arguments – the number of eggs n and the number of trys m – you should calculate maximum scyscrapper height (in floors), in which it is guaranteed to find an exactly maximal floor from which that an egg won’t crack it.
Which means,
You can throw an egg from a specific floor every try
Every egg has the same, certain durability – if they’re thrown from a certain floor or below, they won’t crack. Otherwise they crack.
You have n eggs and m tries
What is the maxmimum height, such that you can always determine which floor the target floor is when the target floor can be any floor between 1 to this maximum height?
Examples
height 0 14 = 0 height 2 0 = 0 height 2 14 = 105 height 7 20 = 137979
Data range
n <= 20000 m <= 20000
راه حل:
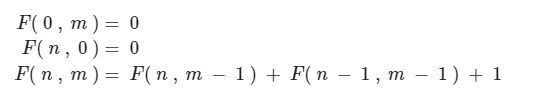
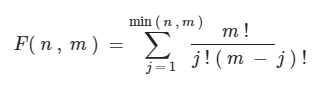
import java.math.BigInteger;
import java.util.HashMap;
import java.util.Map;
public class Faberge {
public static BigInteger height(BigInteger n, BigInteger m) {
Map<BigInteger, BigInteger> map = new HashMap<BigInteger, BigInteger>();
BigInteger result = BigInteger.ZERO;
for (BigInteger i=BigInteger.ONE; i.compareTo(n) != 1; i = i.add(BigInteger.valueOf(1))) {
BigInteger beforeValue = map.containsKey(i.subtract(BigInteger.ONE)) ? map.get(i.subtract(BigInteger.ONE)) : BigInteger.valueOf(1);
BigInteger sorat = beforeValue.multiply(m.subtract(i).add(BigInteger.ONE));
BigInteger makhraj = i;
map.put(i, sorat.divide(makhraj));
result = result.add(map.get(i));
}
return result;
}
}import java.math.BigInteger;
public class Faberge {
public static BigInteger height(BigInteger n, BigInteger m) {
int eggs = n.intValue();
int falls = m.intValue();
if (eggs>falls) return height(m, m);
// Number of binomial coefficients we will calculate (no need to compute more than half of them
// since C(falls,k)=C(falls,n-k), and no need to compute more than the number of eggs)
int coeffs = Integer.min(falls/2+(falls%2),eggs);
// Array that's storing the binomial coefficients C(falls,k), i.e. one line of Pascal's triangle (truncated)
BigInteger[] a = new BigInteger[coeffs+1];
// First column of Pascal's triangle is always 1
a[0] = BigInteger.ONE;
for(int k = 1; k<=falls && k<=coeffs; k++)
// Formula for getting C(falls,k) from C(falls,k-1)
a[k] = a[k-1].multiply(BigInteger.valueOf(falls-k+1)).divide(BigInteger.valueOf(k));
// Now we sum them up
BigInteger res = BigInteger.ZERO;
for(int k = 1; k <= eggs; k++) res = res.add((k>coeffs)?a[falls-k]:a[k]);
return res;
}
}import java.math.BigInteger;
//the solution is so simple, but the proof is so complicated
public class Faberge {
public static BigInteger height(BigInteger n, BigInteger m) {
BigInteger h = BigInteger.ZERO;
BigInteger a = BigInteger.ONE;
for (int e = 1; e <= n.intValue(); h = h.add(a), e++)
a = a.multiply(m.add(BigInteger.valueOf(1 - e))).divide(BigInteger.valueOf(e));
return h;
}
}import java.math.BigInteger;
public class Faberge {
private static BigInteger MOD = BigInteger.valueOf(998244353);
public static BigInteger height(BigInteger n, BigInteger m) {
if (n.compareTo(BigInteger.ZERO)==0 || m.compareTo(BigInteger.ZERO)==0) return BigInteger.ZERO;
if (n.compareTo(m) > 0) return BigInteger.TWO.modPow(m, MOD).subtract(BigInteger.ONE);
BigInteger h = m;
BigInteger binom = m;
for (BigInteger i = BigInteger.TWO; i.compareTo(n) <= 0; i = i.add(BigInteger.ONE)) {
binom = binom.multiply(m.add(BigInteger.ONE).subtract(i))
.divide(i);
h = h.add(binom);
}
return h;
}
}import java.math.BigInteger;
public class Faberge {
public static BigInteger height(BigInteger n, BigInteger m) {
int ni = n.intValueExact();
int mi = m.intValueExact();
if (ni == 0)
return BigInteger.ZERO;
if (ni >= mi)
return BigInteger.valueOf(2).pow(mi).subtract(BigInteger.ONE);
BigInteger s = BigInteger.ZERO;
BigInteger b = BigInteger.ONE;
for (int i = 1; i <= ni; i++) {
b = b.multiply(BigInteger.valueOf(mi + 1 - i)).divide(BigInteger.valueOf(i));
s = s.add(b);
}
return s;
}
}
import java.math.BigInteger;
import java.util.stream.IntStream;
import static java.math.BigInteger.ONE;
import static java.math.BigInteger.ZERO;
public final class Faberge {
public static BigInteger height(final BigInteger n, final BigInteger m) {
return BigInteger.valueOf(2).pow(m.intValue()).subtract(ONE)
.subtract(overdueAttempts(n, m));
}
private static BigInteger overdueAttempts(final BigInteger n, final BigInteger m) {
return IntStream.rangeClosed(0, m.subtract(n).intValue() - 1)
.parallel()
.mapToObj(k -> binomial(m.intValue(), k))
.reduce(ZERO, BigInteger::add);
}
private static BigInteger binomial(final Integer top, final Integer k) {
Integer min = Math.min(k, top - k);
return IntStream.rangeClosed(top - min + 1, top)
.parallel()
.mapToObj(BigInteger::valueOf)
.reduce(ONE, BigInteger::multiply)
.divide(factorial(min));
}
private static BigInteger factorial(final Integer k) {
return IntStream.rangeClosed(2, k).parallel().mapToObj(BigInteger::valueOf).reduce(ONE, BigInteger::multiply);
}
}
import java.math.BigInteger;
public class Faberge {
public static BigInteger height(BigInteger n, BigInteger m) {
BigInteger temp = BigInteger.ONE, rpta = BigInteger.ZERO;
for (BigInteger i = BigInteger.ONE; i.compareTo(n) <= 0; i = i.add(BigInteger.ONE)) {
rpta = rpta.add(temp = temp.multiply(m.subtract(i).add(BigInteger.ONE)).divide(i));
}
return rpta;
}
}
