مساله:
پروفسور چمبولیارد به تازگی نوع جدیدی از مواد مغناطیسی را کشف کرده است. وی ذرات این ماده را در جعبه ای ساخته شده از جعبه های کوچک که در سطرهای K و ستون های N مرتب شده اند ، به عنوان نوعی ماتریس دو بعدی K x N که K و N اعداد صحیح مثبتی هستند، قرار داد.او فکر می کند محاسباتش نشان دهنده نیرویی است که ذره در جعبه کوچک (k ، n) وارد می کند:
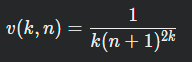
مجموع نیروی اعمال شده توسط ردیف اول با k = 1 برابر است با:
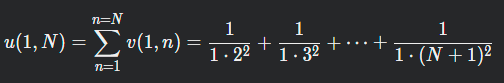
می توانیم با k = 2 و سپس k = 3 و غیره ادامه دهیم و در نظر بگیریم:
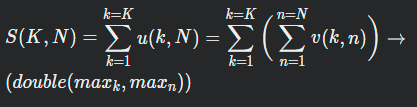
وظیفه:
آیا می توانیم برای کمک به پرفسور تابعی برای محاسبه بنویسیم که اعداد اعشاری maxk, maxn را به عنوان ورودی بگیرد و نتیجه که به صورت عدد اعشاری هست را برگرداند ؟ (به صورت doubles(maxk, maxn) = S(maxk, maxn))
تجربیات نشان می دهد که وقتی maxk و maxn به اندازه کافی بزرگ باشند ، جواب می تواند چیزی در حدود 0.7 باشد.
مثال ها:
doubles(1, 3) => 0.4236111111111111 doubles(1, 10) => 0.5580321939764581 doubles(10, 100) => 0.6832948559787737
نکته ها:
- در عبارت u(1,N) مقدار . عمل ضرب را انجام می دهد
- کوتاه یا گرد نکنید: به نتیجه در “نمونه آزمایش ها” نگاه کنید.
- پیوند به نماد سیگما
Professor Chambouliard hast just discovered a new type of magnet material. He put particles of this material in a box made of small boxes arranged in K rows and N columns as a kind of 2D matrix K x N where K and N are postive integers. He thinks that his calculations show that the force exerted by the particle in the small box (k, n) is:
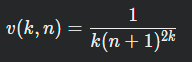
The total force exerted by the first row with k = 1 is:
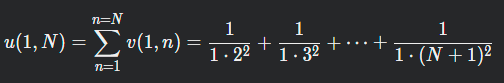
We can go on with k = 2 and then k = 3 etc … and consider:
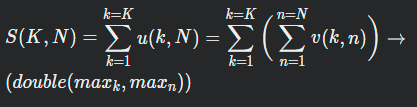
Task:
To help Professor Chambouliard can we calculate the function doubles that will take as parameter maxk and maxn such that doubles(maxk, maxn) = S(maxk, maxn)? Experiences seems to show that this could be something around 0.7 when maxk and maxn are big enough.
Examples:
doubles(1, 3) => 0.4236111111111111 doubles(1, 10) => 0.5580321939764581 doubles(10, 100) => 0.6832948559787737
Notes:
– In u(1, N) the dot is the multiplication operator.
– Don’t truncate or round: Have a look at the testing function in “Sample Tests”.
راه حل ها:
import static java.util.stream.IntStream.range;
import static java.lang.Math.pow;
class Magnets {
public static double doubles(int maxk, int maxn) {
return range(1, maxk+1).mapToDouble(k -> range(1, maxn+1).mapToDouble(n -> 1 / (k * pow(n+1, 2*k))).sum()).sum();
}
}class Magnets {
public static double doubles(int maxk, int maxn) {
double result = 0;
for(int k = 1; k <= maxk; ++k) {
for(int n = 1; n <= maxn; ++n) {
result += 1./(k * Math.pow(n + 1, 2*k));
}
}
return result;
}
}import java.util.stream.*;
class Magnets {
public static double doubles(int maxk, int maxn) {
return DoubleStream
.iterate(1, (i)->i+1.)
.limit(maxk)
.reduce(0, (sumk, k) -> sumk + DoubleStream
.iterate(1, (i)->i+1.)
.limit(maxn)
.reduce(0, (sumn, n) -> sumn + Math.pow(1./(n+1.), 2.*k) / k)
);
}
}class Magnets {
public static double doubles(int maxk, int maxn) {
double doubles = 0;
for(int k = 1; k <= maxk; k++)
for(int n = 1; n <= maxn; n++)
doubles += 1 / (k * Math.pow(n+1, 2*k));
return doubles;
}
}class Magnets {
public static double doubles(int maxk, int maxn) {
return s(maxk, maxn);
}
private static double s(int K, int N) {
double s = 0;
for (int k = 1; k <= K; k++) {
s += u(k, N);
}
return s;
}
private static double u(int k, int N) {
double u = 0;
for (int n = 1; n <= N; n++) {
u += v(k, n);
}
return u;
}
private static double v(int k, int n) {
return 1 / (k * Math.pow((n + 1), 2 * k));
}
}
