ویرگول: فیلم معروف Interstellar یا “درمیان ستارگان” اثر کریستوفر نولان، علاوه بر کارگردانی بینظیر و موزیک متن فراموشنشدنی، از دقّت علمی بالایی نیز برخوردار است و مفاهیم مختلفی از فیزیک نوین را به تصویر میکشد.
در صورتی که هنوز این فیلم را ندیدهاید، بهتر است ابتدا این مطلب را مطالعه نمایید و سپس به سراغ فیلم بروید. داستان این فیلم رابطهی بسیار تنگاتنگی با نظریهی نسبیت داشته که اوّلینبار توسّط آلبرت آینشتاین پایهگذاری شد. میتوان گفت که این نظریه به توضیح چگونگی رفتار کیهان میپردازد.

فرض کنید در حال حرکت با اتوموبیلی هستید و ۹۰km/h سرعت دارید و اتومبیل دیگری نیز با سرعت ۶۰km/h پشت سر شما و همان راستا به دنبال شما در حال حرکت است. در همین حین اتوموبیل سوّمی نیز با سرعت ۱۰۰km/h از هردوی شما جلو میزند. بدیهیست که شما گذر آن اتوموبیل را نسبت به خود با سرعت ۱۰km/h میبینید و حتّی چند لحظهای نیز فرصت دارید که به رانندهی اتومبیل سوّم سلام کنید؛ در حالی که رانندهی دوّم، گذر اتومبیل سوّم از کنار خود را با سرعت ۴۰km/h دیده و ممکن است حتّی نتواند چهرهی رانندهی آن را نیز به درستی ببینید!
رابطهی میان سرعت با اتّساع زمان یک رابطهی خطّی نمیباشد و هرچه به نور نزدیکتر شود نرخ اتّساع زمان نیز بیشتر میشود. به بیان دیگر، حتّی زمانی که شما در حال دویدن هستید نیز زمان برایتان کمی بیشتر از شخصی که ثابت ایستاده است کش میآید؛ امّا این تفاوت زمانی در حدّ کسر بسیار کوچکی از ثانیه است و به حدّی ناچیز بوده که اصلاً نیازی نیست در محاسبات روزمرّه به عنوان یک فاکتور در نظر گرفته شود.
مفاهیم بالا بخشی از نسبیت خاص است و مربوط به زمانی میشود که حرکتی نسبی با سرعت ثابت انجام پذیرد. پس از اثبات آن، انیشتین سالهای بسیاری از عمر خود را صرف تعمیم دادن این نظریه کرد تا بتواند رفتار کیهان در حرکات شتابدار و همچنین در میدانهای گرانشی را توصیف کند (اصولاً شتاب و گرانش از ماهیت یکسانی برخوردارد؛ چرا که خود گرانش باعث ایجاد شتاب میشود.) و در نهایت آن را تحت عنوان نظریهی نسبیت عام به اثبات رساند. آنچه از این نظریه برای درک فیلم Interstellar لازم است بدانید این است که هر جسم دارای جرم و دارای گرانشی، کیهان اطراف خود را خم میسازد و طبعاً باعث اتّساع زمان نیز میشود. بدین صورت که هرچقدر تحت میدان گرانشی شدیدتری باشید، زمان نیز برای شما کندتر میگذرد.
امّا تحت میدانهای گرانشی بسیار قوی اتّساع زمان به طرز ملموسی افزایش پیدا میکند و یکی از قویترین منابع گرانشی نیز سیاهچالههای فضایی میباشند. امّا سیاهچاله چیست؟

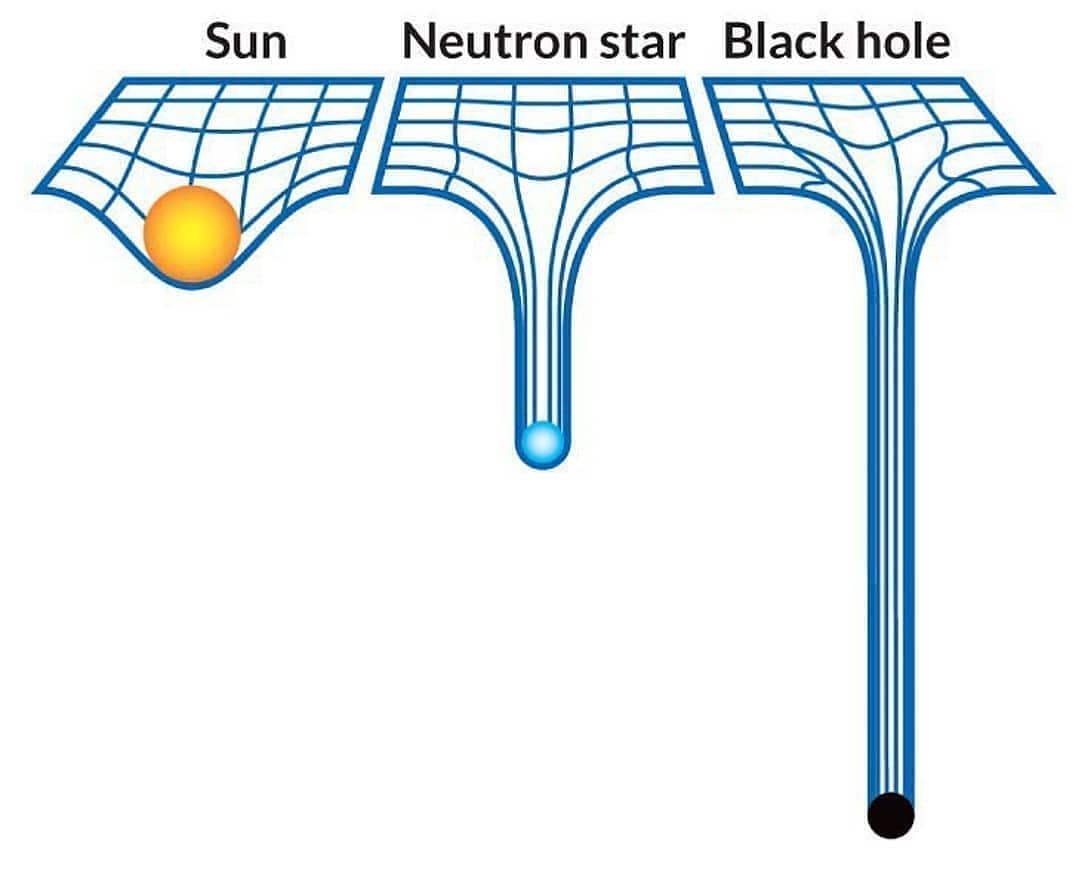
با تجمّع جرم بسیار زیادی از هیدروژن در یک نقطه، ستارهای متولّد میشود. این جرم زیاد، گرانش بسیاری ایجاد کرده تمایل دارد ستاره را در هم فروریخته و فشرده کند. امّا واکنش همجوشی هستهای میان اتمهای تشکیل دهندهی ستاره، انرژی عظیمی آزاد کرده که تمایل به منفجر کردن ستاره از درون را دارد. این دو نیرو در تقابل هم ستاره را در تعادل نگه میدارند. با کاهش هیدروژن (و هلیوم) موجود در ستاره و تبدیل آن به عناصر سنگینتر در طی این واکنش، به تدریج نیروی گرانش شروع به غلبه کردن میکند. در نهایت عمر ستاره به پایان رسیده و منفجر میشود و آنچه از آن باقی میماند، به شدّت فشرده میشود.
از طرفی سیاهچالهها معمولاً گازهای موجود در اطراف را به سمت خود کشیده و معمولاً تودهای از گاز حول آنها تشکیل میشود و با سرعت زیادی به چرخش در میآیند. این فرآیند میتواند امواج الکترومغناطیس (از جمله نور) و گرما ایجاد کند. پس میتوانیم منظومهای داشته باشیم که مرکز آن یک سیاهچاله بوده و اطراف آن سیاهچاله نیز سیّاراتی در گردش باشند و توسّط گرمای تولید شده از گازهای اطراف سیاهچاله گرم شوند.
سیاهچالهها به اندازهای گرانش دارند که اتّساع زمان در اطراف آنها به شدّت ملموس میشود. به گونهای که ممکن است هر ساعت در اطراف آنها به درازای چندین سال، دهه یا قرن به درازا انجامد.
تجسّم خم شدن یک فضای سهبعدی (طول، عرض، ارتفاع) در ذهن ما موجودات سهبُعدی و یا نمایش آن روی کاغذ ناممکن است و فقط به زبان ریاضیات میتوانیم راجع به آن سخن بگوییم. امّا صرفاً برای درک بهتر، میتوان بجای سه بُعد، فضا را دو بُعدی (فقط شامل طول و عرض) در نظر گرفت و از بُعد سوّم (ارتفاع) جهت نمایش خمیدگی دو بُعد دیگر بهره جست. در این صورت، حاصل تصویری به شکل زیر میشود – ستارهای که فضای اطراف خود را خم کرده است و سیّارهای نیز در مدار آن قرار دارد.
آینشتاین برای آزمایش عملی این موضوع که آن را روی کاغذ و توسّط ریاضیات به اثبات رسانده بود، اینطور پیشبینی کرد که از آنجا که نور همیشه در یک خطّ مستقیم حرکت میکند، زمانی که قسمتی از خود کیهان دچار خمیدگی شده باشد، نور عبوری از آن قسمت نیز باید به واسطهی این خمیدگی، دچار انحراف مسیر شود. برای مثال میدان گرانشی اطراف خورشید باید نور ستارگانی که در پشت خورشید قرار گرفتهاند را منحرف کرده و باید بتوان در لبهی خورشید، ستارههایی را مشاهده کرد که اصولاً در آن لحظه باید در پشت خورشید قرار گرفته باشند.
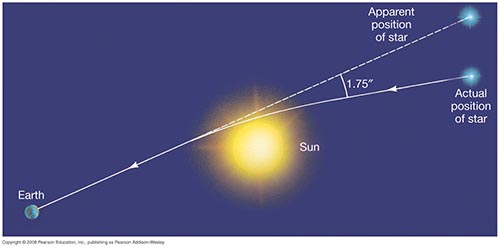
او برای انجام این آزمایش ناچار شد تا زمان وقوع یک خورشیدگرفتگی صبر کند و در نهایت نیز از این آزمایش توانست مهر تأییدی بر نتیجهی نظریهی خود بزند. امّا امروزه با فرستادن تلسکوپهای فضایی در خارج از اتمسفر زمین، دیگر نیاز نیست منتظر خورشیدگرفتگی بمانیم. همچنین از این پدیده به عنوان تکنیکی برای اجسام بسیار دور استفاده میکنیم (تکنیک Gravitational Lensing).
یک سیاهچاله نیز به واسطهی گرانش زیاد خود، نور پشت سرش را به شدّت خم کرده و همچون یک عدسی غولپیکر عمل میکند.
امّا درون یک سیاهچاله واقعاً چه خبر است و پس از گذر بیبازگشت از افق رویداد، واقعاً چه اتّفاقی میافتد؟ پاسخ این سؤال را نمیدانیم؛ ولی هرچه هست، قوانین فیزیک درون یک سیاهچاله با قوانین فیزیکی که ما میشناسیم متفاوت خواهد بود. ممکن است سیاهچالهها، دالانهایی بسته نباشند بلکه به واسطهی گرانش بسیار زیاد خود طوری فضا-زمان را دستخوش تغییر قرار دهند که به دریچهای به ابعاد دیگری از کیهان، زمانهای دیگری از کیهان و یا حتّی کیهانهایی موازی را باز کنند. هیچ مطمئن نیستیم.
شاید فضای سهبُعدیای که در آن زندگی میکنیم، توسّط پوستهای دوبُعدی احاطه شده باشد و ممکن است روی این پوستهی دوبُعدی نیز جهانی دوبُعدی برپا باشد و حتّی موجوداتی دو بُعدی نیز ساکن آن باشند. این موجودات دوبُعدی، همچون کاراکترهای بازیهای ویدئویی قدیمی هستند و برای آنها فقط دو راستای چپ-راست و بالا و پایین وجود دارد. شما باید بتوانید از بالا به آنها بنگرید در حالی که برای آنها هرگز بالا یا پایینی تعریف نشده است که سر خود را در آن سو بچرخانند. برای آنها چیزی بنام حجم تعریف نشده است و فقط طول و مساحت را حساب میکنند. مهندسینشان انتگرالی بالاتر از انتگرال دوگانه به دردشان نمیخورد.
حال موجوداتی چهاربُعدی و… را تصوّر کنید! آنها میتوانند از ابعادی بالاتر به ما بنگرند در حالی که ما هرگز نمیتوانیم گردنمان را در راستای آن ابعاد بچرخانیم و به آنان بنگریم. حتّی ممکن است زمان نیز آنگونه که تصوّر میکنیم نباشد. شاید زمان نیز صرفاً یک سراشیبی باشد که فضای سهبُعدی ما در حال سُر خوردن به روی آن است و جلو رفتن زمان نیز درواقع همین حرکت فضا بر روی زمان باشد.
امّا برگردیم به نسبیت عام. گفتیم که مطابق این نظریه، فضا میتواند خم شود. همان فضای دوبُعدیای که از آن صحبت شد را در نظر بگیرید و آن را به صورت یک پارچهی کِشباف تجسّم کنید. این پارچه را میتوان کشید، فشرده کرد، خم کرد، تا کرد و یا مچاله کرد. فرض کنید آیدا و بابک دو موجود دوبُعدیِ ساکن این کیهان دوبَُعدی هستند و در دو نقطه به فاصلهی ۱۰۰۰ کیلومتر زندگی میکنند.
پس هرکدام که بخواهد دیگری را ببیند، باید نزدیکترین مسیر را که خطّ مستقیمی به فاصلهی ۱۰۰۰ کیلومتر است طی کند. امّا شما به عنوان یک موجودِ سهبعدیِ که علاوه بر x و y، توانایی حرکت در محور z را نیز دارید، میتوانید لحظهای کنار آیدا باشید و سپس فقط با طی کردن ۱ سانتیمتر در راستای z، خود را به بابک برسانید و هردو را انگشت به دهان کنید که چطور با این سرعت توانستید بین این دو نقطه جابهجا شوید!
چرا که حتّی اگر آیدا به طریقی بتواند با سرعت نور به سمت بابک حرکت کند، به ۰.۰۰۰۰۰۳۳۳۳ ثانیه زمان نیاز دارد تا این مسیر ۱۰۰۰ کیلومتری را طی کنید در حالی که شما بجای دستیابی به سرعت نور، اگر فقط با سرعت ۳۰۰۰ متر بر ثانیه این مسیر ۱ سانتیمتری را طی کنید، زودتر از آیدا به مقصد خواهید رسید!
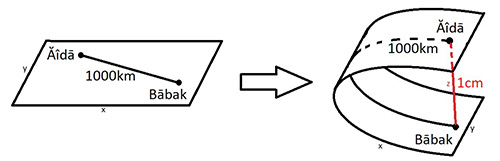
برای آنها چیزی بنام محور z تعریف نشده و آنها اگر کیهانشان را آنقدر خم کنیم که آن فاصلهی قرمزرنگ به صفر رسیده و موقعیت ایندو دقیقاً روی هم منطبق شود چه؟ در این صورت نزد آیدا و بابک دروازهای عجیب گشوده شده است که هرکدام با ورود به آن میتوانند از موقعیت دیگری – جایی ۱۰۰۰ متر آنطرفتر – سر در بیاورند؛ آن هم بدون صرف هیچ زمانی! به این مفهوم، کرمچاله گفته میشود. به همین شکل اگر دو نقطه از فضای سهبعدی ما نیز در راستای بُعد چهارم روی یکدیگر خم شود، برای ما نیز کرمچالهای ایجاد میشود که با ورود به آن میتوانیم از نقطهی دیگر سر درآوردیم؛ حتّی اگر این دو نقطه در دو سر کیهان قرار داشته باشند!

دانستن مفاهیمی که تاکنون گفته شد برای درک فیلم زیبای Interstellar تا حدود زیادی کفایت میکند. شاید اکنون که دید بازتری نسبت به مفاهیم علمی آن پیدا کردید، ارزش یک بار دیدن مجدّد را داشته باشد!